Comment dimensionner cette poutre treillis à l'ELU et ELS?
Tout d'abord un petit mot sur les structure treillis...

le principe d'un treilli expliqué par Michel...
Dimensionnement à l'ELU
Commençons par dimensionner cette structure à l'ELU:
Nous allons déterminer les sections des membrures de la structure afin d'assurer la résistance de celle-ci.
Dimensionner à l'ELU revient à comparer un Effort (Force, Moment,...) Résistant à un Effort Sollicitant


Les semelles (parties horizontales des poutres treillis) des poutres reprennent:
- de la traction en partie supérieure (F)
- de la compression en partie inférieure (F)
Ces forces sont égales (en valeur absolue) aux réactions d'appuis horizontales R1x et R2x

Ces deux forces sont égales (principe d'équilibre) et sont espacées de la hauteur du bâtiment-pont (a).
Elles constituent donc un couple de forces ou un Moment:
F x a

Le moment est maximum à l'appuis. Que vaut-il?
Nous connaissons pl (la charge linéaire calculée précédemment) et L la longueur du porte-à-faux.
M = pl x L² / 2 donc: F = (pl x L² / 2) / a
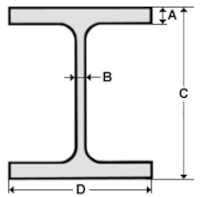
Supposons que les semelles sont constituées de profilé H comme celui-ci. Quelle doit être la dimension de ce H pour résister au moment sollicitant?
Calcul de la sollicitation (Fsd)
Nous avons calculé précédemment la valeur de l'action linéaire majorée (pld) dans le cas du caclul à l'ELU

pld (ELU) = 126 kN/m
L = 24.8 m
a = 8.8 m
Fsd = 126 kN/m x ( (24.8 m)² /2 ) / 8.8 m = 4 403 kN
Calcul de la résistance (Frd)
Vérification pour une HEA 200
L'effort Résistant Minoré d'une HEA 200 est égale à la
contrainte minorée 235 N/mm² multipliée par la surface d'acier que présente ce profilé (dans sa section)
A = ?
Pour connaitre cette section nous allons consulter le catalogue des profilés.
Nous y voyons par exemple que la surface d'acier de la section est de 53.8 cm² pour une HEA200 soit:
A = 5380 mm²
Testons une HEA 200
Attention, la charge linéaire majorée est reprise par deux poutres treillis. Donc chaque poutre treillis reprend la moitié de la sollicitation Fsd. Ou encore, Fsd est repris par deux poutres H.
Nous allons prendre en compte 2 fois la surface d'une HEA 200 (soit 107.6 cm²)
Frd = 235 N/mm² x 5 380 mm² x 2 = 2 528.6 kN
Ce profilé est trop "faible". Il nous faudrait deux profilés dont la surface totale serait de l'ordre de
4 403 kN / 235 N/mm² =187 cm²
Soit des profilés dont la surface de section serait de 94 cm² chacun.
Retour au catalogue: Cela correspond à une HEA 280
Testons une HEA 280
Frd = 235 N/mm² x 2 x (9730 mm)² = 4 573 kN
Frd (4 573 kN) > Fsd (4 403 kN): OK!
Nous aurions pu comparer non pas des efforts F mais des Moments.
Cela donnerait alors ceci:
Msd = 126 kN/m x (24.8 m)² / 2 = 38 748 kNm
Vérification pour HEA 280
Mrd = 235 N/mm² x (9730 mm)² x 2 x 8 800 mm = 70 243 280 000 Nmm = 40 243 kNm
Mrd > Msd: OK!
Remplaçons les HEA 280 par des sections pleines
Si nous remplaçons les poutres HEA 280 par des sections carrées pleines en acier, il nous faudra simplement respecter une surface de 94 cm² par profilé.
Soit des profilés carrés de 9.6 cm de côté.
Arrondissons à 10 cm

étape suivante: ELS