Comment dessiner l'allure du diagramme des moments sur base de la déformée?
Rappel: Forces et Moments en tant qu'efforts internes

Nous allons nous intéresser aux efforts qui agissent à l'intérieur de la matière. Prenons une barre; que ce soit une poutre ou une colonne et isolons (par le principe de la coupe) un tronçon dans cette barre. Les efforts qui nous intéressent sont ceux qui agissent sur ce tronçon ou élement au droit des coupures.
Force interne
Une Force Interne dans un élément tend à allonger ou raccourcir l'élément en question.

Moment interne
Un Moment Interne dans un élément tend à fléchir l'élément en question.

Le Moment se calcule comme une Force multipliée par un bras de levier.
Dès que la déformée de l'élément étudier se courbe, il y a présence d'un Moment.
Fibres tendues et comprimées: Le Moment crée donc une flexion / une courbure qui d'un côté de l'élément tend les fibres et de l'autre les comprime.
C'est exactement ce qui se passe dans la botte de spaghettis (notre poutre): les "fibres" du haut sont tendues et celles du bas, comprimées.
Dessiner la déformée des poutres / portiques / colonnes
Pourquoi relier les moments à la déformée d'une poutre? Simplement parce-qu’il n'y a pas de moment sans déformation. Si un tronçon de poutre subit un moment interne, alors la poutre va se déformer transversalement en se "courbant" (alors qu'une force axiale sur une poutre va la déformer longitudinalement en "l'allongeant"). De cette courbure on peut déduire l'allure générale (non quantitative) du diagramme des moments.
Dessiner l'allure de la déformée d'une poutre - rappel
Si vous éprouvez des difficultés à dessiner la déformée que prendra par exemple une poutre sous une charge particulière alors cette section est pour vous.
Suivez d'abord la vidéo 1 pour apprendre à faire une déformée, regardez ensuite la vidéo 2 pour "voir" de vraies déformées et comparer les résultats.
1 Dessiner l'allure de la déformée
Pour apprendre à dessiner rapidement l'allure d'une déformée d'une poutre ou plus généralement d'une structure quelconque. L'idée est simple: transformer la structure en un mécanisme en rajoutant des rotules là où sont appliquées les forces (les forces de réactions d'appuis compris).
Exercices complémentaires
2 Illustration de la déformation d'un portique
Pour visualiser des déformées réelles.
4 règles permettant de déduire l'allure du diagramme des moments à partir de la déformée
4 règles suffisent pour déterminer le diagramme des moments en partant de la déformée d'une poutre. Nous allons les découvrir au travers de l'analyse de 2 poutres. La première est une poutre encastrée-libre chargée à son extrémité. Commençons par représenter cette poutre sous la forme de son schéma statique:
Allure du diagramme des moments pour une poutre encastrée-libre chargée à son extrémité

Prenons une poutre encastrée - libre de 6 m de long et retenant à son extrémité une charge de 100 kg
Pour rappel, le moment maximum de cette poutre vaut
M = P x L
Soit dans notre cas: M = 10 kN x 6m = 60 kN.m

On peut tout de suite tracer l'allure de la déformée de cette poutre:
L'extrémité libre va descendre sous la charge.
Au droit de l'encastrement l'axe de la poutre ne subira pas de rotation (ni de translation bien évidemment).

Règle n°1: Si la déformée de la poutre présente une courbure (différente de la courbure éventuelle initiale), alors c'est que celle-ci est soumise à un Moment interne.
Dit autrement:
S'il y a courbure, alors il y a moment.

Grâce au principe de la coupe nous allons déterminer le moment en 4 points sur cette poutre. Ensuite nous tracerons le diagramme des moments en reliant ces points.

C'est quoi encore le principe de la coupe?
Pour info, rappel etc, vous trouverez ci-contre un exemple d'exploitation du principe de la coupe basé sur le sens du moment.
Il n'utilise aucune convention de signe, ce qui vous oblige à une seule chose: être cohérent dans le calcul. La seule convention reste celle qui impose le dessin du Moment côté Fibre tendue.
Si vous respectez cette convention elle donnera exactement le même résultat que d'autres méthodes basée sur des conventions de signe <0 et >0

Analysons le résultat sur notre poutre.
Le moment le plus grand est à l'encastrement:
Le moment est maximum là où ça cassera!
Le moment est nul à l'extrémité libre de la poutre car le bras de levier est nul.

Règle n°2: Le moment sera toujours nul à une extrémité rotulée (rotule, rouleau ou libre) d'une poutre.
CONVENTION:
Par convention nous dessinerons le diagramme des moments du côté des fibres tendues (ici la déformée nous montre que les fibres tendues sont sur la partie supérieure de la poutre, les moments seront donc dessinés dans la partie supérieure de celle-ci (au-dessus donc de l'axe de la poutre).

Les charges ponctuelles induisent un diagramme des moments linéaire.
ici M = F x l
l étant la distance séparant la force externe F de l'endroit où l'on calcule le moment
En D le Moment = 0 et
la flèche est maximale
En A le Moment est max et
La flèche est nulle
La courbure (y'') de la poutre est fonction de M: y" = M/(EI)
E étant le module de Young et I l'inertie.
Donc la courbure de notre poutre est max en A et nulle en D
Allure du diagramme des moments pour une poutre encastrée-libre chargée uniformément

Prenons la même poutre et chargeons-là cette fois avec une charge répartie de 200 Kgf/m.
Calculons ensuite les moments en chacun de nos points.
Pour rappel, le moment maximum de cette poutre vaut
M=pl²/2 Soit dans notre cas: M = 2 kN/m x (6m)² /2 = 36 kNm


Les charges linéaires induisent un diagramme des moments quadratique: celui-ci suit une courbe et non plus une droite

Règle n°3:
Entre deux charges ponctuelles, le diagramme des moments suivra une droite. Le long de charge réparties/linéaires, le diagramme dessinera une courbe (diagramme quadratique)
Règle n°4:
Par équilibre, la somme des moment en un point est nulle et donc les moments sont "continus". ils varient de façon continue et leur diagramme ne peut donc contenir de tronçon vertical
(comme dans l'image de droite ci-dessous).
Les schémas ci-dessous respecte cette règle: le moment d'un côté du noeud est égal au moment de l'autre côté de ce noeud. L'équilibre est respecté.

Le schémas ci-dessous n'est pas possible car il ne respecte cette règle: M1 devrait être égal à M2 et M3 égal à M4 (pas de "tronçon vertical" possible dans le diagramme excepté si un moment externe est appliqué en ce point)

Déterminons ensemble et à partir de ces 4 règles l'allure du diagramme d'une poutre

Soit une poutre sur 2 appuis chargée ponctuellement.
Traçons directement sa déformée.
Première question: la poutre est-elle fléchie et donc soumise à un Moment interne?

Deuxième question: Peut-on déterminer les points du diagramme où le Moment est nul?

Troisième question: Peut-on tracer l'allure du diagramme?

Remarquez l'analogie avec le diagramme des moments d'une poutre encastrée-libre!
Cette analogie se démontre par le principe de la coupe. Elle est également valable pour une charge linéaire (et non ponctuelle).
Et pour finir, quelques diagrammes, déformées et valeurs typiques
Diagrammes et déformées
Cette partie vous sera très utile pour continuer dans le jeu Breaking Beams: vous y verrez synthétisé les diagrammes des moments et les déformées de quelques cas typiques. Enregistrez-les bien!

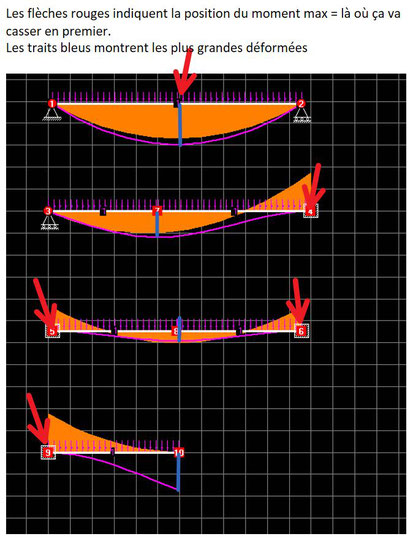
Voici quelques poutres toutes chargées avec la même charge linéaire.
Les appuis "triangle" représentent des rotules, les triangle sur petits rouleaux, des appuis à rouleaux et les carrés des encastrements.
En orange: le diagramme des moments, en violet la déformée.
On voit que le moment maximum croît (et que la flèche maximale décroît) de la poutre bi-appuyée (cas 1) vers la poutre bi-encastrée (cas 3)
On voit aussi que la position du moment maximum est différente dans chaque cas et que celui-ci se trouvera "attiré" par des liaisons plus "rigides" (comme les encastrements versus les appuis rotulés).
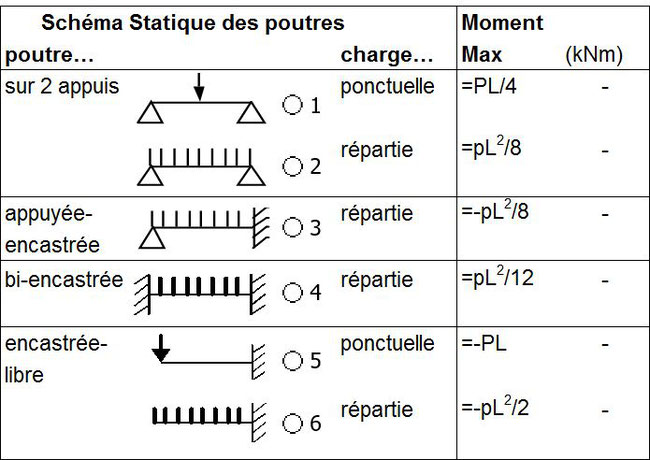
Formules permettant de calculer les moments max de quelques schémas statiques courants.