
Notion de sécurité
La « sécurité » sur les actions
Les actions définies ci-avant sont des actions « théoriques », la norme les qualifie d’actions caractéristiques (elles sont généralement reprises avec un indice k).
Dans la réalité ces actions seront parfois dépassées et la « sanction » ne pourra bien entendu pas être la ruine de la structure. Pour cela on introduit des sécurités.
La sécurité sur les actions se traduit par une majoration de celles-ci. La majoration des actions est également destinée à couvrir les approximations, les simplifications qui sont inévitablement faites lors du calcul des efforts internes dans les éléments qui constituent la structure.
Les majorations des actions à prendre en compte sont définies par la norme. En première approximation on se limitera aux coefficients suivants :

Les actions permanentes (poids propre "pp", poids des parachèvements aussi appelées "surcharges pemanentes", "g") étant mieux connues le coefficient de majoration qui les affecte est inférieur à celui correspondant aux actions variables.
Les actions ainsi majorées seront utilisées pour le calcul à l’ELU. Pas de majoration pour le caclul ELS.
Le fluage et le bois

Sous l'action des charges de longues durées, on assiste à un accroissement progressif des déformations. C'est ce qu'on appelle le fluage

Pour tenir compte du fluage dans les éléments en bois on majorera la flèche sous les actions permanente de 80%
Pour la commodité du calcul il sera plus simple de calculer une flèche élastique considérant des actions permanentes multipliées par 1.8 et des actions variables non majorées
f = K * (actions permanentes *1.8 + actions variables)*L³/(E *I)
La flèche obtenue est comparée à la flèche maximale admissible.
Le fluage et le béton

Pour tenir compte du fluage dans les éléments en béton on doublera la flèche sous les actions permanentes.
Pour la commodité du calcul il sera plus simple de calculer une flèche élastique considérant des actions permanentes multipliées par 2:
f = K * (actions permanentes*2 + actions variables)*L³/(E *(b*h³/12)*0.60)
Attention à ne pas être trop pessimiste. Il ne faut se préoccuper que de la « flèche dangereuse ».
Dans le cas des ossatures en béton armé le poids propre est important. Vu que les parachèvements ne sont réalisés qu’après décoffrage, il serait trop défavorable de prendre en compte la flèche élastique relative au poids propre dans la détermination de la flèche « dangereuse ». On ne tiendra donc compte que de la flèche due au fluage sous poids propre
La formule de la « flèche dangereuse » est donc :
F « dangereuse » = K * (actions du poids propre+ action parachèvement*2 + actions variables)*L³/ (E *(b*h³/12)*0.60)
On ne tient compte ainsi de la flèche due au fluage sous le poids propre, de la flèche élastique et de la flèche de fluage sous les charges permanentes et de la flèche élastique sous les charges variables.
La flèche obtenue est comparée à la flèche maximale admissible.
Si la flèche maximale autorisée n’est pas respectée il faut augmenter l’inertie de la poutre.
Récapitulatif

La « sécurité » sur les résistances des matériaux
Comme nous l’avons vu on tient compte de « sécurités » en majorant les actions et en minorant les résistances.
Pour déterminer les caractéristiques mécaniques des matériaux on procède à des essais qui sont le plus souvent des essais de traction et/ou de compression. Les résultats de ces essais présentent une certaine dispersion.
La figure de gauche représente l’histogramme d’une série d’essais. Soit le nombre d’essais donnant une certaine valeur en fonction de cette valeur.
Nombre d'essais
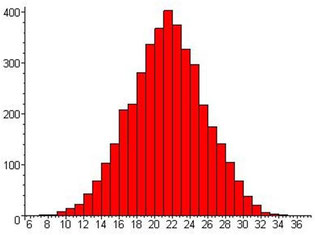
Valeur mesurée
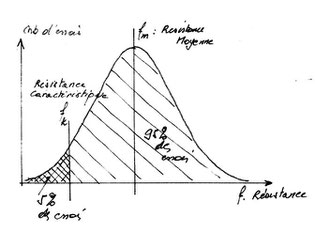
La graphique de droite est la courbe issue de cet histogramme.
Supposons par exemple qu’il s’agit de la résistance à la traction (f) d’un matériau.
fm est alors la résistance moyenne et fk la résistance « caractéristique » c’est celle que l’on est certain d’obtenir dans 95% des cas. Les valeurs « caractéristiques » des caractéristiques mécaniques matériaux sont celles qu’on est certain d’obtenir dans 95% des essais. Ce sont ces valeurs « caractéristiques » qui seront utilisées pour la vérification des sections des éléments de structure.
Bien entendu, on ne va pas « fermer les yeux » sur les 5% de cas où la résistance est inférieure à la résistance caractéristique. C’est pour cela notamment qu’on va minorer les résistances « caractéristiques » pour obtenir les résistances de calcul qui seront utilisées pour la vérification de la capacité portante des éléments de structure. Cette « minoration » des résistances tient donc compte de la dispersion des caractéristiques mécaniques des matériaux utilisés, mais aussi de l’éventuelle différence entre les matériaux des éprouvettes d’essais et les matériaux qui seront utilisés dans la structure, des éventuels écarts dimensionnels des sections et des approximations faites lors du calcul des contraintes.
Le coefficient de minoration va donc dépendre du matériau et de la précision de la réalisation des éléments de structure.
Coefficient de minoration de la résistance de l’acier de profilés laminé (cas courants)
1.00
Vu les qualités de leur fabrication, on est certain de leurs caractéristiques mécaniques et géométriques et donc on ne minore pas leur résistance, le coefficient de minoration vaut donc 1.
Coefficient de minoration de la résistance du bois résineux courant (CL18)
1.30
Pour les bois voir norme NBN EN 1995
Coefficient de minoration de la résistance du bois lamellé collé courant (GL22)
1.25
Il y a plus de certitude pour ce qui est des caractéristiques du bois lamellé collé que pour celle du bois de charpente courant, donc on réduit le coefficient de minoration
Coefficient de minoration de la résistance du béton (pour béton armé)
1.50
Il y a plus d’irrégularité dans la fabrication du béton que dans la fabrication de l’acier. Le coefficient de minoration sera donc plus important. Pour des bétons très contrôlés en usine par exemple ce coefficient pourrait être réduit. Par contre pour des bétons réalisés dans des conditions plus précaires, il devrait être augmenté. La valeur de 1.5 correspond à un béton préparé en centrale à béton agrée.
Coefficient de minoration de la résistance de l’acier (pour béton armé)
1.15
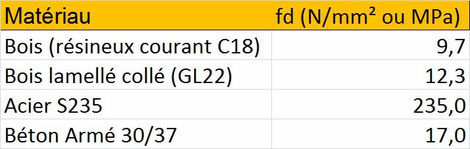
Valeurs de résistance pour les matériaux usuels

