Comment calculer l'inertie?

Comment calculer l'inertie?

1- L'inertie: une notion purement géométrique

Le "Moment quadratique" ou "inertie" (nous utiliserons couramment ce dernier terme pour désigner cette notion) est une caractéristique de la géométrie d'une surface.
Elle correspond à une surface (inscrite dans un plan) multipliée par le carré de la distance séparant un point quelconque du plan au centre de gravité de cette surface.

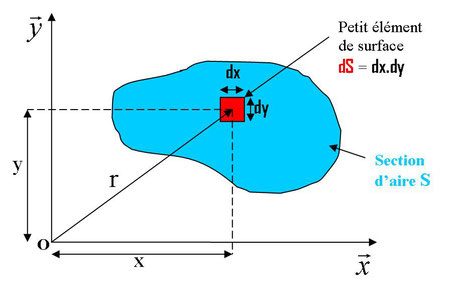
Voici une représentation de cette définition (from wikipedia). Dans le plan xy, si on multiplie dS par r² on obtient un Moment Quadratique.

Mais qu'est-ce qui a bien pu motiver des mathématiciens à "pondre" une notion pareille et dans quel but?

2- L'inertie: définition générale

Le moment quadratique ou moment d'inertie est une grandeur qui caractérise la géométrie de la section (de la poutre dans le cadre de ce cours, c'est-à-dire la surface perpendiculaire à la portée de la poutre).
Elle s'exprime en unité de longueur élevé à la 4ieme puissance car elle correspond à la somme (ou intégrale) de surfaces multipliées par un bras de levier élevé au carré.

Si on avait l'habitude de l'exprimer en cm4 jusqu'à un passé proche, on lui préfère actuellement le mm4.

3- Calculs pratiques: le cas d'une poutre rectangulaire pleine

Les poutre en bois sont en général de section rectangulaire et elle sont pleine (contrairement au tubes an acier par exemple qui sont creux). Les formules de calcul des inerties et des I/v de telles poutres sont simples.

Calcul de l'inertie

I = b.h³/12

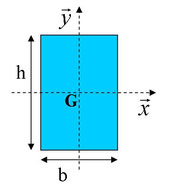
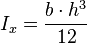
$I_x= \frac {b \cdot h^3}{12}$
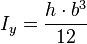
$I_y= \frac {h \cdot b^3}{12}$

Pourquoi 2 inerties?

L'inertie Ix est relative à la flexion de la poutre dans un plan perpendiculaire à x (par exemple dans le cas d'actions // à y)

L'inertie Iy est relative à la flexion de la poutre dans un plan perpendiculaire à y (par exemple dans le cas d'actions // à x)

Dans notre cas (et dans la plupart des cas d'ailleurs) Ix > Iy

On dira que Ix est l'inertie de l'axe fort et Iy l'inertie de l'axe faible.

Une colonne flambera toujours suivant son axe faible d'inertie.

La RAIDEUR (opposé à flexibilité, souplesse) d'une poutre est proportionnelle à son inertie.

Par exemple si on double le I, on double la raideur de la poutre.

Calcul du I/v

calcul du I/v d'une poutre rectangulaire pleine

Ix=b.h³/12

par définition: vx=h/2

Donc:

Ix/vx = (b.h³/12)/(h/2) = b.h²/6

Exemple

Prenons une poutre de (b=) 12cm sur (h=) 20cm

Son inertie forte (axe x) = 12 x 20³ / 12 = 20³ = 8 000 cm4 ou 80 000 000 mm4

Son I/v (fort) = 12 x 20² / 6 = 400x2 = 800 cm3 ou 800 000 mm3

Son inertie faible (axe y) = 20 x 12³ / 12 = 2 880 cm4 ou 28 800 000 mm4

Son I/v (fort) = 20 x 12² / 6 = 480 cm3 ou 480 000 mm3

La RESISTANCE (la capacité à ne pas casser) d'une poutre est proportionnelle à son I/v.

Par exemple si on double le I/v, on double la résistance de la poutre.

4- Le cas des poutres en "i".

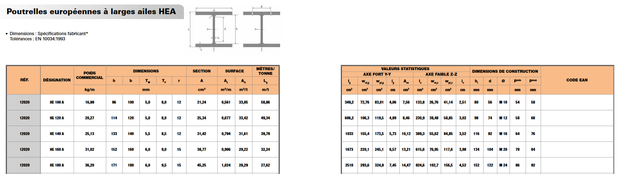
Les poutres en i et H sont généralement en acier (on trouve également en bois ou en béton). leur inertie et i/v se retrouvent dans des cataloques (voir ci-dessous).
On ne les calcule donc généralement pas. Néanmoins il est parfois utile de pouvoir calculer l'inertie d'une telle poutre. Voici comment on procède.

Prenons une poutre en acier de type HEA200. Sa largeur est de 20cm, sa hauteur de 19cm.

Ses semelles ont une épaisseur de 10mm et son âme une épaisseur de 6.7mm

Nous allons d'abord simplifier le profil de la poutre en 3 rectangles assemblés: 2 pour les semelles et un pour l'âme.

Ensuite nous allons considérer que ce profilé en "h" est constitué d'un rectangle plein de 19cm de large sur 20cm de haut (en bleu) dont on a soustrait deux rectangles jaunes plus petits.

Pour calculer l'inertie du profilé H nous allons calculer l'inertie du rectangle plein (bleu) et ensuite lui soustraire l'inertie de la matière enlevée soit celle des 2 rectangles jaunes.

1- calculons l'inertie du rectangle plein bleu

L'inertie du rectangle plein

I1= bh³/12 avec

b = 20 cm et h = 19 cm

I1 = 20x19³ / 12

= 11 431.7 cm4

2- calculons l'inertie des rectangles pleins jaunes

L'inertie des rectangles pleins jaunes

I2= 2x bh³/12 avec

b = 9.7 cm et h = 17 cm

I2 = 2 x (9.7x17³ / 12)

= 7 942.7 cm4

3- déduisons l'inertie de notre profil H

L'inertie du profilé H

I = I1 - I2

= 3 489 cm4

Si on regarde l'Inertie forte d'une HEA 200 dans un catalogue on trouvera

I = 3 692 cm4

La petite différence est due aux "congés": les arrondis qui relient l'âme aux semelles.

Pour obtenir le I/v correspondant divisez le I par la demi hauteur soit ici 19 cm/2 et vous obtiendrez:

3692/9.5=389cm³

5- Catalogues des profilés en acier

Les poutres en acier sont produites par de nombreux fabricants. Cependant, dans un souci de normalisation, ils répondent à des dimensions et qualités d'acier bien précises et normées.

Ces données sont reprises dans des catalogues commerciaux comme vous en trouverez beaucoup sur le net (l'illustration ci-dessus en est un exemple).

Les voici reprises dans ce catalogue en ligne.

Les données principales qui nous intéressent sont:

leur nom (colonne A)
leur poids propre (colonne B)
leurs dimensions principales (colonne C et D)
leur inertie I suivant l'axe fort (colonne J)
leur module d'inertie I/v suivant l'axe fort (colonne J), repris ici sous l’appellation Wely