
Comment dimensionner une colonne pour éviter le flambement?
Introduction
Lancez la vidéo et aller au début de la séquence "Colonne" qui démarre à 12:46.
Michel Provost nous parle du fonctionnement des colonnes. L'expérience qu'il réalise sur des colonnes de même section illustre particulièrement bien l'effet des appuis (encastrés, rotulés) sur ce qu'on appelle la longueur de flambement.
Quand Euler s'y met...

Le mathématicien suisse Euler démontra la relation suivante:
Pcrit = π² E I / Lfl²
Où
Pcrit est la charge au-delà de laquelle le flambement
apparait
E est le module de Young du matériau
I est l'inertie du profilé (inertie faible bien sûr)
Lfl est la longueur de flambement de la colonne (elle dépend de la
longueur mais aussi des appuis), elle est notée dans la littérature Lfl ou Lo ou Lk
Voyons l'influence de chacun des termes de l'équation
Si l'Inertie augmente, la charge maximale admissible augmente
Le flambement apparaît quand, pour des raisons d'irrégularités de la matière et des forces appliquées, une colonne se met à fléchir sous une charge parallèle à son axe, alors qu'une poutre fléchira sous l'action de charges perpendiculaire à son axe.
Le flambement est finalement un problème de flexion, et il est logique que l'inertie joue un rôle important dans le phénomène.
Si E augmente, la charge maximale admissible augmente
A section égale, si on remplace par exemple une colonne en bois par une colonne en acier (de même géométrie), la charge qu'elle pourra reprendre sera beaucoup plus grande, ce qui est logique.
Si Lfl augmente, la charge maximale admissible diminue

En fonction des appuis, qu'ils soient articulés ou encastrés, le flambement apparait plus ou moins vite: vous pouvez le voir dans la vidéo d'introduction.
On voit dans le schéma ci-contre l'influence de ces liaisons sur la longueur de flambement (notée Lk dans ces schémas), facteur important déterminant Pcrit
.
Dans la formule d'Euler, la charge critique diminue quand la longueur de flambement de la colonne augmente ce qui est logique: plus la colonne est élancée plus la charge critique diminue.
En pratique, la formule d'Euler n'est plus directement utilisée pour dimensionner une colonne. En effet, la charge critique de flambage d'Euler ne pourrait être atteinte que dans le cas idéal d'une barre parfaitement rectiligne et homogène, sans aucune imperfection géométrique et chargée sans aucune excentricité. Dans la réalité, ces imperfections ont pour conséquence de mener à un flambage précoce de la barre, sous-estimé par la formule d'Euler.
Remarque pour les architectes: Ce qui suit est facultatif et explique dans le détail le principe de dimensionnement d'une colonne par l'ingénieur. Tout le processus de calcul selon la norme est intégré dans le fichier Prédim dont l'utilisation est expliquée dans la vidéo qui clôture cette page.
Le calcul selon la norme
Le dimensionnement des colonnes suivant les normes actuelles repose sur les notions suivantes:
1- la longueur de flambement (L0) (cette longueur est la longueur de la colonne réduite ou augmentée en fonction des conditions de liaison à ses extrémités)
2- les caractéristiques géométriques de la section exprimées par le rayon de giration (i). Le rayon de giration exprime l’éloignement de la matière par rapport au centre de gravité de la section.
Les rayons de giration des différents profilés métalliques (I, H, tubes,...) sont donnés dans les tableaux et catalogues reprenant les caractéristiques de ces profilés.
3- Le rapport longueur de flambement / rayon de giration appelé l’élancement structural de la colonne (λ). Le risque de flambement est d’autant plus important que l’élancement est grand.
En première approximation on peut considérer que si l’élancement (λ) est inférieur ou égal à 25 il n’y a pas de risque de flambement. Alors le calcul de la section colonne est identique à celui de la suspente.
Une méthode simple serait donc de respecter toujours cette condition. Toutefois cela ne serait architecturalement pas raisonnable, les sections des colonnes ainsi dimensionnées étant très importantes.
4- Les minorations des résistances liées au matériau et au risque de flambement. Ces minorations sont fonction de l'élancement et grandiront avec celui-ci. Un élancement de 1 correspondant à l'absence de minoration.
L0 = 2L / 0.5L / L / 0.7L
en fonction des liaisons de la colonne (comme chez Euler)
i = √(I / Ω)
où,
I est l'inertie
Ω la surface de matière dans la section
Pour une colonne carrée (b=le côté du carré)
I = (b^4)/12
Ω = b²
Donc:
i = b/√12
Pour une colonne creuse circulaire:
i = 1/4 x √(D²-d²)
où D = le diamètre extérieur et
d = le diamètre intérieur
λ = L0 / i
Si λ < 25: pas de risque de flambement
Etapes du calcul
Le processus de calcul est le suivant :
1- Déterminons l’effort P à reprendre par la colonne en différenciant l’effort dû aux charges permanentes et l’effort dû aux charges variables
2- Déterminons l’effort de calcul Pd (à l'ELU) = action permanente *1.35 + action variable * 1.5
3- Déterminons la longueur de flambement en tenant compte de la hauteur géométrique et des conditions de liaison aux extrémités de la colonne
4- Choisissons un profilé, déterminons l’aire et le rayon de giration de sa section
5- Déduisons la contrainte de calcul réduite (fdR)qui tient compte de la réduction liée au risque de flambement (voir tableau ci-après)
6- Détermination de la résistance de calcul Rd de la colonne : Rd=Ω*fdR (Réduite)
7- Il faut que Rd≥ Pd
Si le résultat n’est pas satisfaisant on recommence avec un autre profilé et ainsi de suite.
CE QUI SUIT EST CE QUE "PREDIM" FAIT POUR VOUS... Ce n'est pas à retenir.
Colonnes Acier
Les colonnes métalliques sont le plus souvent des profilés, des tubes,... quasi jamais des sections pleines. En effet, ces dernières ne sont pas performantes, la matière n’est pas assez éloignée du centre de gravité.
Dans la méthode décrite dans les normes on détermine les sollicitations qui agissent sur une section et on les compare à la résistance de celle-ci.
Ces sollicitations sont les sollicitations majorées considérant les coefficients de majoration des actions, elles sont appelées sollicitations de calcul (Sd, Pd... - indice d de design).
La résistance de la section est établie considérant les résistances de calcul réduite qui intègrent les minorations des résistances liées au matériau et au risque de flambement (cfr tableau). Ce sera la résistance de calcul Rd (indice d de design).
Colonnes Bois
En bois nous aurons des sections pleines. Pour respecter le critère de l’élancement inférieur ou égal à 25 les dimensions devraient être les suivantes :
Ainsi une colonne bi-articulée de 3 m de haut et de section carrée devrait avoir au moins 41 cm de côté ce qui n’est pas raisonnable ! Là aussi nous allons appliquer une réduction de contrainte pour tenir compte du risque de flambement.
1. Considérons d’abord une colonne en compression sans risque de flambement.
La contrainte qui ne pourra pas être dépassée est la contrainte caractéristique du bois multipliée par un coefficient réducteur (pour chargement permanent) et divisée par le coefficient de minoration.
Il y a différentes essences de bois et les coefficients varient notamment en fonction des conditions d’hygrométrie. Dans l’esprit de ce manuel, vu que l’objectif est de donner un ordre de grandeur de la section nous nous limitons à deux types de bois et une classe d’humidité.
Pour le « bois résineux courant »(C18) La contrainte à ne pas dépasser (contrainte de calcul) est d’environ
18 N/mm² X 0.7 (coefficient réducteur chargement permanent) / 1.30 (coefficient de minoration) = 9.7 N/mm²
Pour le « bois lamellé collé courant » (GL22) La contrainte à ne pas dépasser (contrainte de calcul) est d’environ
22 N/mm² X 0.7 (coefficient réducteur chargement permanent) / 1.25 (coefficient de minoration) = 12.3 N/mm²
2. S’il y a risque de flambement (à partir d’un élancement λ de 30) ces contraintes sont réduites (cfr tableau).
Colonnes béton

Considérons d’abord une colonne en compression sans risque de flambement.
Le problème est comparable à celui du bois mais il est rendu plus compliqué vu que nous sommes en présence d’un matériau composite fait de béton et d’acier.
La capacité portante du béton armé sera influencée par la proportion d’armatures. La résistance de l’acier étant supérieure à celle du béton, plus la section d’armature sera importante plus la capacité portante de la colonne sera importante à section globale constante.
Nous avons donc deux matériaux, le béton et l’acier dont les modules de Young et les contraintes caractéristiques (fck)
sont très différents.
Plusieurs nuances d’acier pour béton armé et de béton sont utilisées. Dans l’esprit de ce manuel, vu l’objectif de donner un ordre de grandeur de la section, nous nous limitons à un type d’acier pour béton armé et un type de béton, tous deux courants : du béton 30/37 et de l’acier BE400

Acier BE 400 : résistance caractéristique = 400 N/mm²
Contrainte de calcul d’un acier BE400: 400/1.15 (coefficient de minoration) = 348 N/mm²
Remarquez que les deux diagrammes ne sont pas à la même échelle: si on devait représenter le diagramme du béton 30/37 sur celui de l'acier on obtiendrais la petite courbe rouge près de l'origine du graphique

Béton 30/37 : résistance caractéristique = 30 N/mm² (cette résistance est obtenue par écrasement d’un cylindre de 15 cm de diamètre et de 30 cm de hauteur, le second chiffre, 37, correspond à l’écrasement d’un cube de 20 cm de côté)
Contrainte de calcul d’un béton 30/37 = 30 x 0.85 (coefficient réducteur pour mise en charge de longue durée)/1.5 (coefficient de minoration) = 17 N/mm²
Prédim intègre la philosophie de dimensionnement imposée par les Eurocodes. Il vous permet de pré-dimensionner rapidement des colonnes en suivant quelques étapes clé.
A l’ELU, le béton et l’acier travailleront dans leur palier de plasticité. Le tableau suivant donne la contrainte moyenne dans la section en fonction du type de béton et du % d’armature.

De plus nous considérerons qu’il y a 2% d’acier dans les colonnes
La contrainte moyenne dans la colonne à l’ELU sans risque de flambement sera donc de :
« Contrainte de moyenne de calcul » = 98 % X 17 N/mm² + 2% X 348 N/mm² = 23.6 N/mm²
S’il y a risque de flambement (élancement λ supérieur à 25) cette contrainte est réduite et le processus de calcul est le suivant :
1- Détermination de l’effort P à reprendre par la colonne en différenciant l’effort dû aux charges permanentes et l’effort dû aux charges variables
2- Détermination de l’effort de calcul Pd = action permanente *1.35 + action variable * 1.5
3- Détermination de la longueur de flambement en tenant compte de la hauteur géométrique et des conditions de liaison aux extrémités de la colonne.
4- Choix d’une section, détermination de l’aire et du rayon de giration de sa section
5- Déduction de la contrainte moyenne à ne pas dépasser (contrainte moyenne de calcul réduite) en tenant compte de la réduction liée au risque de flambement (voir tableau ci-dessous)
6- Détermination de la résistance de calcul Rd de la colonne Rd=Ω*fdR (Réduite)
Il faut que Rd ≥ Pd
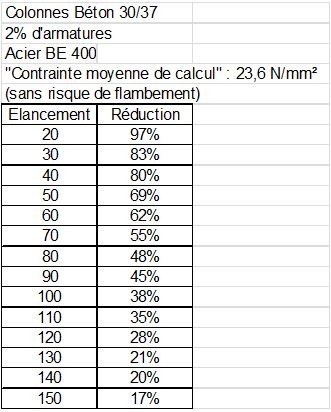
Le tableau ci-après donne, pour un une colonne en béton 30/37 avec 2% d’acier BE400, les coefficients de réduction de la « contrainte moyenne de calcul » en fonction de l’élancement de la colonne
Exemple: un élancement de 40 implique une contrainte de 23.6 N/mm² x 80% = 18.9 N/mm²
Le pré-dimensionnement des colonnes sur prédim
Comment pré-dimmensionner une colonne sur Prédim?
Le tuto suivant explique comment utiliser l'onglet colonne dans la feuille de calcul Prédim.



