Inertie

Lien entre efforts intérieurs et section d'une poutre

Reprenons le cas simple et courant d'une poutre sur deux appuis soumise à une charge ponctuelle.

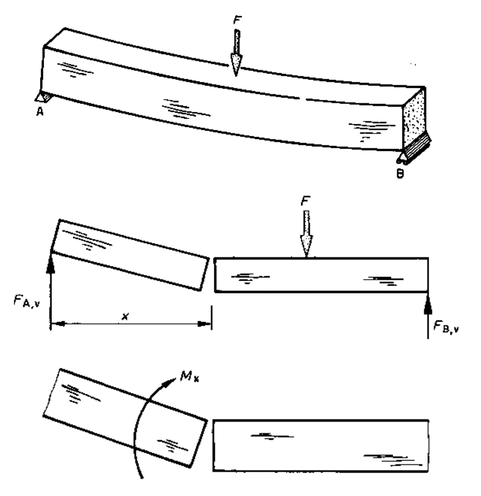
Observons le diagramme des moments M : au fur et à mesure qu'on s'éloigne des appuis, l'intensité des moments augmente dans les sections de la poutre, jusqu'à atteindre le maximum au point d'application de la force.

Si on se rappelle que le moment est lié à la tendance à la rotation du tronçon gauche de la poutre par rapport à son tronçon droit, cela signifie que la tendance à la rotation des fragments de poutre les uns par rapport aux autres va aller en augmentant jusqu'au point d'application de la force ponctuelle. Cette tendance à la rotation des éléments les uns par rapport aux autres, due aux charges extérieures, entraînera une déformation de la poutre, plus ou moins grande en fonction de la capacité de la poutre à lui résister. Cette déformation s'appelle la flexion.

Abordons à présent l'étude de notre poutre d'un autre point de vue. Si on observe une poutre de section rectangulaire (hauteur h et base de largeur b), on peut l'assimiler à un ensemble de longues fibres parallèles (de la longueur de la poutre). Dans le cas de la poutre ci-contre, la déformée observée de la poutre sera la suivante :

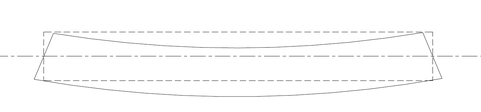
La partie supérieure de la poutre se raccourcit, elle est comprimée. Tandis que la partie inférieure s’allonge, et est donc tendue. La partie centrale de la poutre que l’on appelle fibre neutre conserve sa longueur initiale, cette partie n’est ni tendue ni comprimée.

On peut donc dire, que suite à la mise en charge de la poutre, des contraintes de compression σ apparaissent dans les fibres supérieures, et que des contraintes de traction apparaissent dans les fibres inférieures. Nous développerons plus en détail cette notion de contrainte dans la notion qui leur est dédiée, mais considérons ici que l'allongement de chaque fibre longitudinale qui constitue la poutre (de son bord gauche à son bord droit dans la poutre ci-dessus) sera proportionnel à la contrainte qu'il subit.

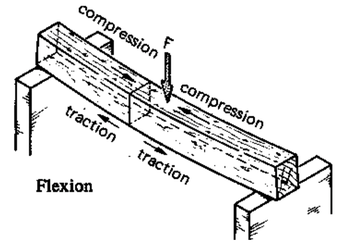
Au niveau de la fibre neutre, il n’y a aucune déformation ni contraintes σ=0.

Si comme on l'a dit ci-dessus, on suppose que les déformations sont proportionnelles aux contraintes, alors on obtient une répartition  triangulaire des contraintes. 

Plus on s’éloigne de la fibre neutre, plus les déformations et donc les contraintes sont grandes.

Les compressions et les tractions maximales se situent respectivement au niveau des faces supérieures et inférieures de la poutre. Ces contraintes sont perpendiculaires au plan de la section, puisqu'elles correspondent à un étirement ou à un raccourcissement des fibres de la poutre.

Nous l'avons vu précédemment, les cas de charges rencontrés dans le cadre de ce cours (forces réparties ou concentrées sur poutres isostatiques) nous amènent des efforts intérieurs, dans les sections de la poutre, en M et T, (N étant nul).

Sur base de ce que nous venons de voir, nous pouvons donc dire que dans ces cas de charges, N étant nul et M différent de zéro, la résultante des contraintes de compression et la résultante des contraintes de traction constitueront un couple de forces !

La répartition de ces contraintes sera donc du type ci-dessous.

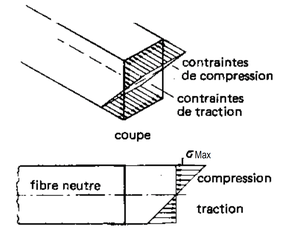
Les contraintes de compression et de traction sont maximales dans les fibres supérieures et inférieures. Appelons-les "σmax". Si on pousse l'observation, on remarque que si F augmente, les déformations augmentent, donc, les contraintes augmentent. 

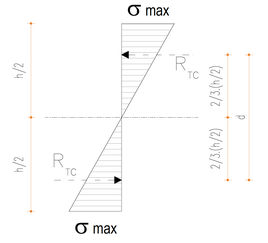
La résultante de traction et de compression vaudra donc :

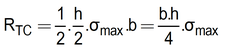
(puisque les contraintes s'exercent sur toute la surface de coupe de hauteur h et de base b).

Le moment résultant vaudra donc quant à lui l'intensité de cette résultante multipliée par la distance entre les deux forces constituant le couple, soit :

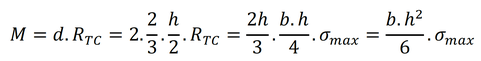
Quels enseignements pouvons-nous à présent tirer?

1. Sur les dimensions
Reprenons la formule liant le moment dans une section avec les dimensions de cette section et la contrainte en traction et compression maximale qui y apparaît.
Pour rappel, ce moment est un effort intérieur que subit la poutre suite à sa mise en charge. Elle devra donc y résister. 
Le moment résistant maximum que nous appelerons le "Moment admissible" que notre poutre pourra opposer sera donc:

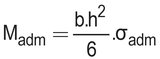
Celui-ci est donc aussi fonction de h et de b. On aura donc intérêt à choisir une poutre plus haute que large (puisque h apparaît au carré dans cette formule) pour que les poutres résistent mieux à la flexion. Plus concrètement, pour la poutre ci-dessous, la flexion sera moindre dans le cas gauche.

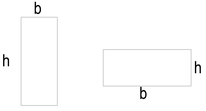
Le terme "(b‧h^2)/6" dépend exclusivement des dimensions de la section de la poutre. On l'appelle le "Module d'inertie". C'est le grand enjeu de cette notion.
Notons bien que cette valeur n’est valable que pour les poutres à section rectangulaire pleines.

Nous allons voir à la suite comment ce module d'inertie se calcule pour une section quelconque.

Le module d'inertie qualifie la résistance et la raideur de la section d'une poutre. Plus l'inertie de la section sera grande, moins la poutre soumise à la flexion aura tendance à fléchir, et rompre.


2. Sur les matériaux
σmax est la contrainte maximale à la traction et à la compression que le matériau va subir dans une section donnée (mais toujours dans les fibres extrêmes).
Un matériau sera caractérisé par des contraintes à la compression et à la traction admissibles maximales, mesurées en laboratoire.

On les nomme "σadm". Au delà de cette limite, le matériau se rompt. Il faudra donc toujours que σmax qui apparaît dans le matériau suite à la mise en charge soit inférieure à σadm.

Dans notre cas précis, comment et où cela va-t'il se produire?

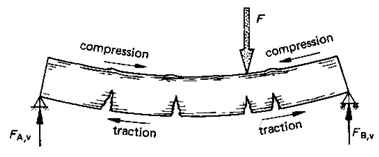
Dans la fibre extrême, autour du point d'application de la force, car c'est là que les contraintes qui apparaissent seront les plus grandes. On risque ainsi une fissuration qui remonte dans le matériau depuis le bas, ou qui descend depuis le haut suivant les σadm en compression et en traction du matériau.


Certains matériaux résistent bien à la traction et à la compression, c'est le cas de l'acier ;

d'autres, bien à la traction et mal à la compression, c'est le cas du bois.

D'autres, bien à la compression et pas à la traction, c'est le cas du béton.

Dans le cas de ce matériau artificiel, le danger est grand d'un déchirement des fibres inférieures et de fissures qui remontent jusqu'à découper la poutre en deux.

Pour contrer ce défaut, on joint au béton dans ses fibres inférieures un matériau résistant bien à la traction : l'acier.

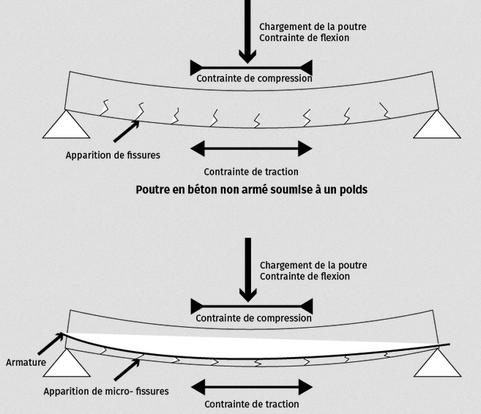
 On parle alors de béton armé.

Dans la photo ci-dessous, les huit  "barres à béton" métalliques (aussi appelées "armatures métalliques") sont placées en renfort dans les fibres basses pour reprendre la traction que le béton est incapable d’assumer.

 Le choix du matériau pour une poutre est donc primordial dans son comportement sous charges.


3. Sur les formes
Les fibres extérieures (supérieures et inférieures) étant les plus sollicitées, on aura intérêt à les renforcer au maximum. Si on pousse le raisonnement plus loin avec comme objectif une économie de matière, on aura intérêt à retirer la matière la moins sollicitée de la section, c’est-dire, celle proche de la fibre neutre.

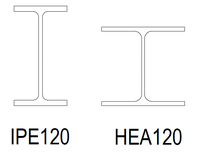
En combinant ces deux raisonnements, en travaillant avec un matériau comme l’acier (très résistant à la traction et à la compression), on comprend les formes des sections des profilés ci-dessous en acier.

Ce que nous appellerons l'INERTIE porte également le nom de "Moment quadratique" ou de "Moment d'inertie".

Le moment quadratique est indispensable pour calculer la déformation des poutres sollicitées en flexion. Il dépend de la forme, de la section de ces poutres (et pas du matériau).

Nous le représenterons par la lettre majuscule "I" que l'on retrouve par exemple dans les formules des flèches maximales des 2 poutres sur 2 appuis représentées ci-après.

Son petit frère, le MODULE D'INERTIE (noté "I/v" ou "w") est aussi très important : il est nécessaire au calcul de la résistance à la rupture des matériaux.

On le retrouve dans la formule qui relie le Moment (interne, de flexion, obtenu via les diagrammes MNT), à la contrainte, comme vu ci-dessus : σ = M / (I/v)