Le câble dimensionné plus tôt sera-t-il assez "raide"?
Nous venons de déterminer la section du hauban en acier S235 afin que celui-ci résiste à la traction dûe au poids du bâtiment. Pour résister à une charge de 976.31 kN il doit faire 72 mm de diamètre.
La question suivante que nous devons nous poser est la suivante: l'effort de traction auquel va être soumis le hauban ne va-t-il pas "trop" allonger celui-ci et rendre le bâtiment inutilisable?
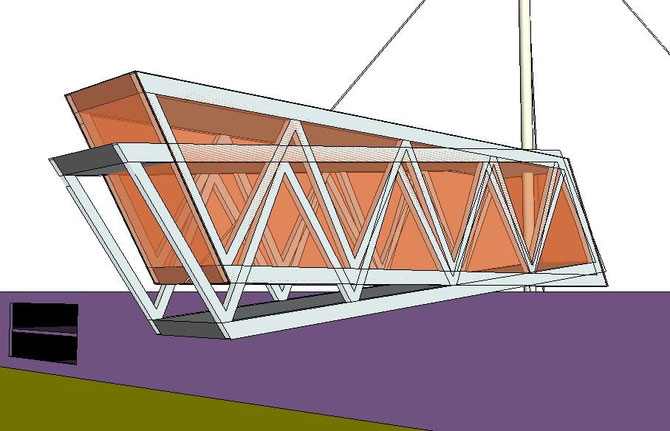
Tous les matériaux (sans exception) s'allongent lorsqu'ils sont soumis à un effort de traction (et se raccourcissent si l'effort est de compression).
Un élastique s'allongera plus qu'une barre d'acier de même section. On dira que l'acier est plus RAIDE que le caoutchouc de l'élastique.

Expérience:
Déterminer le rapport entre l'allongement et la charge (Module de Young)
Quel est le rapport entre l'allongement et la contrainte?
Quel est l'alongement maximum acceptable dans le hauban? Une question de géomètrie...
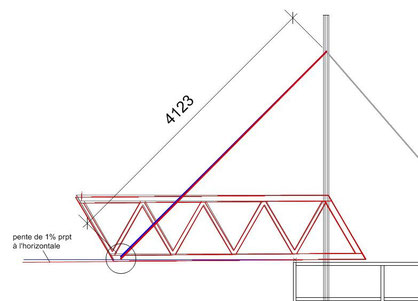
Nous allons imposer que la pente dans le bâtiment pont ne peut dépasser 1%
Cette limite dans la déformation peut être liée à de nombreux critères différents. Le critère qui prévaut ici est d'éviter une pente trop sensible pour les utilisateurs du bâtiment. Considéront que 1% est encore une pente acceptable pour ceux-ci.
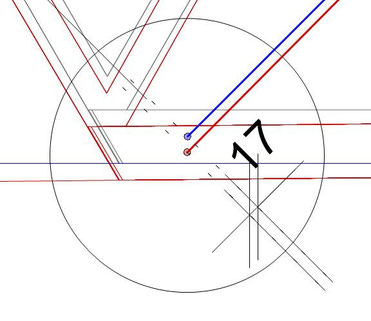
Si on zoom sur la jonction entre le tirant et la structure du bâtiment pont, on peut déterminer graphiquement l'alongement maximum acceptable.
Cet allongement maximal (Delta L) = 17 cm
l'allongement subit < l'allongement acceptable?
Quel allongement, notre hauban dimensionné suivant l'ELU (pour éviter l'a rupture) va-t-il subir?
Est-il égal ou inférieur à l'allongement maximum acceptable?
Calculons cet allongement:
Notre hauban est en acier doux. Il fait 72mm de diamètre afin de limiter la contrainte à 235 N/mm² lorsqu'il doit résister à une traction de 976.31 kN.
Comme
E=sigma / epsilon et que E = 210 000 N/mm²
Avec:
epsilon = Delta L / L
Alors:
epsilon = sigma / E = 235 N/mm² / 210 000 N/mm²
Delta L = epsilon x L = (235 N/mm² / 210 000 N/mm²) x L = (235 / 210 000) x 4123 cm = 4.6 cm
Delta L = 4.6 cm < Allongement max admissible = 17 cm
OK!

Exercices:
1 - Si l'on remplace l'acier doux du hauban par un câble haute résistance, l'allongement est-il acceptable?
Rappel:
σ = 1000 [MPa] et E = 170.000 [MPa
2 - Si ce n'est pas le cas, quelle section de câble haute résistance devrions-nous imposer?
Récapitulatif
1- Nous avons tout d'abord réolut un problème de STABILITE en ajoutant un hauban à l'ensemble.
2- Nous avons ensuite résolut un problème de RESISTANCE en dimensionnant ce hauban pour qu'il résiste à la charge du bâtiment.
3- Nous venons enfin d'aborder le problème de la DEFORMATION en contrôlant l'allongement du hauban.
